replicating omega frequency | Is it real? A buyer's guide to spotting a fake Omega replicating omega frequency Related Reading:• Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007). The Mechanical Universe. New York City: Cambridge University Press. pp. 383–385, 391–395. ISBN 978-0-521-71592-8. See more TSS does add his own touch with gold foil branding and a custom cut orange swing tag, in reference to the recent release. The Shoe Surgeon LV AJ1 is available to order now from their website and is priced at $10,000 each pair.
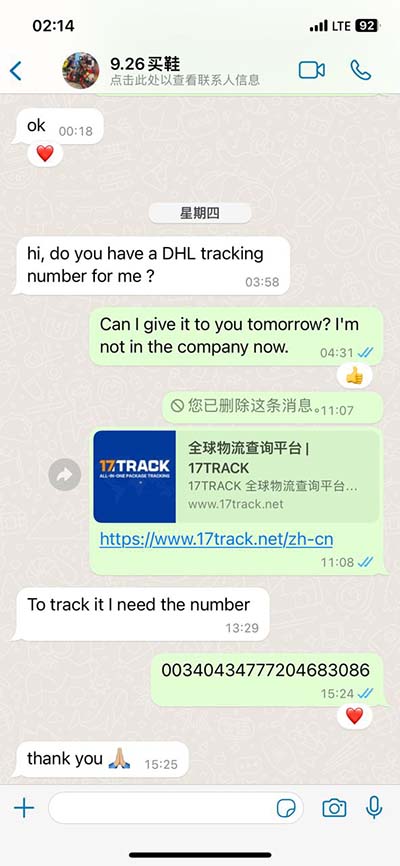
0 · trigonometry
1 · sampling
2 · Why are angular frequencies $\\omega=2\\pi f$ used over normal
3 · What is the significance of angular frequency $\omega$ with
4 · Mechanisms of Theta Plasmid Replication
5 · Is it real? A buyer's guide to spotting a fake Omega
6 · Angular frequency
7 · Amplitude, Frequency, Wave Number, Phase Shift
8 · 9.2: DNA Replication
9 · 6.02 Practice Problems: Modulation & Demodulation
This week on CBS, CSI's D.B. Russell meets CSI: NY's Mac Taylor under far from the best of circumstances -- and TVLine has a first look at the horrific event that sets the two-night.
In physics, angular frequency (symbol ω), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine function (for example, in oscillations and waves). Angular frequency (or . See more
In SI units, angular frequency is normally presented in the unit radian per second. The unit hertz (Hz) is dimensionally equivalent, but by convention it is only used for frequency f, . See moreAlthough angular frequency is often loosely referred to as frequency, it differs from frequency by a factor of 2π, which potentially leads confusion when the distinction is not made clear. See more
Related Reading:• Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007). The Mechanical Universe. New York City: Cambridge University Press. pp. 383–385, 391–395. ISBN 978-0-521-71592-8. See moreCircular motionIn a rotating or orbiting object, there is a relation between distance from the axis, $${\displaystyle r}$$, tangential speed, $${\displaystyle v}$$, and the angular frequency of the rotation. During one period, See more
• Cycle per second• Radian per second• Degree (angle)• Mean motion• Rotational frequency See moreTo get the frequency domain representation of this modulated signal, we replicate the spectrum of the original signal at \(-\Omega_c\) and \(+\Omega_c\), scaling each of these replications by . I wanted to "rediscover" the replication of the signal spectrum by pure algebraic manipulation from ejθ or cos(θ + ϕ). First you have to understand where images come from. . It's just nicer to name \pi f$ term as angular frequency $\omega$,- as it gives dimensions $[\text{rad/s}] \equiv [\text{rad} \cdot \text{Hz}]$. That's why it is sometimes called .
The angular frequency is related to a quantity often labeled f f and also called the frequency by \omega = 2\pi f ω = 2πf. With these new definitions, solutions to the wave equations can be .
The frequency of replication initiation is tightly regulated to facilitate establishment in permissive hosts and to achieve a steady state. The last section of the article reviews how . You could consider omega to be a pure indicator of periodicity in the cycle. Larger omega gives you more rads per second. Larger omega gives you shorter wavelength, and . The reason we use the angular frequency, $\omega$, is because the \pi$ is always present and so to know how quickly the function repeats, i.e. to have an intuitive idea .
The replication of DNA occurs during the synthesis phase, or S phase, of the cell cycle, before the cell enters mitosis or meiosis. The elucidation of the structure of the double .
It should have a unique identifying serial number engraved on the case, which you can check against Omega's records. Fake Omega watches are among the most common kinds of .In physics, angular frequency (symbol ω), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase .To get the frequency domain representation of this modulated signal, we replicate the spectrum of the original signal at \(-\Omega_c\) and \(+\Omega_c\), scaling each of these replications by . I wanted to "rediscover" the replication of the signal spectrum by pure algebraic manipulation from ejθ or cos(θ + ϕ). First you have to understand where images come from. .
Both processes are given from the shift property of the Fourier Transform which states that multiplying a function $x(t)$ in the time domain by $e^{j\omega_c t}$ will shift the . It's just nicer to name \pi f$ term as angular frequency $\omega$,- as it gives dimensions $[\text{rad/s}] \equiv [\text{rad} \cdot \text{Hz}]$. That's why it is sometimes called .The angular frequency is related to a quantity often labeled f f and also called the frequency by \omega = 2\pi f ω = 2πf. With these new definitions, solutions to the wave equations can be .
versace shirt black and gold and king queen
The frequency of replication initiation is tightly regulated to facilitate establishment in permissive hosts and to achieve a steady state. The last section of the article reviews how .$\omega$: Normalized radian frequency. $\omega = \Omega/F_s = 2\pi F/F_s$. Sometimes its units are listed as being radians/sample. Because of aliasing, it is only necessary to study the . You could consider omega to be a pure indicator of periodicity in the cycle. Larger omega gives you more rads per second. Larger omega gives you shorter wavelength, and . The reason we use the angular frequency, $\omega$, is because the \pi$ is always present and so to know how quickly the function repeats, i.e. to have an intuitive idea .
In physics, angular frequency (symbol ω), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase .To get the frequency domain representation of this modulated signal, we replicate the spectrum of the original signal at \(-\Omega_c\) and \(+\Omega_c\), scaling each of these replications by . I wanted to "rediscover" the replication of the signal spectrum by pure algebraic manipulation from ejθ or cos(θ + ϕ). First you have to understand where images come from. .
Both processes are given from the shift property of the Fourier Transform which states that multiplying a function $x(t)$ in the time domain by $e^{j\omega_c t}$ will shift the . It's just nicer to name \pi f$ term as angular frequency $\omega$,- as it gives dimensions $[\text{rad/s}] \equiv [\text{rad} \cdot \text{Hz}]$. That's why it is sometimes called .The angular frequency is related to a quantity often labeled f f and also called the frequency by \omega = 2\pi f ω = 2πf. With these new definitions, solutions to the wave equations can be .
The frequency of replication initiation is tightly regulated to facilitate establishment in permissive hosts and to achieve a steady state. The last section of the article reviews how .$\omega$: Normalized radian frequency. $\omega = \Omega/F_s = 2\pi F/F_s$. Sometimes its units are listed as being radians/sample. Because of aliasing, it is only necessary to study the . You could consider omega to be a pure indicator of periodicity in the cycle. Larger omega gives you more rads per second. Larger omega gives you shorter wavelength, and .
trigonometry
Counter-Strike: Global Offensive. 28 Jul 21. Guides. oofpezz. The Ultimate Guide to the Best CSGO Launch Options. Confused about which launch options to use to optimize your game? Check out our definitive launch options guide to get your game running the best it can.
replicating omega frequency|Is it real? A buyer's guide to spotting a fake Omega